book-notes

Chapter 8 - Greedy algorithms

Greedy algorithm

• Greedy algorithm is simple: at each step, pick the optimal move.

Knapsack problem

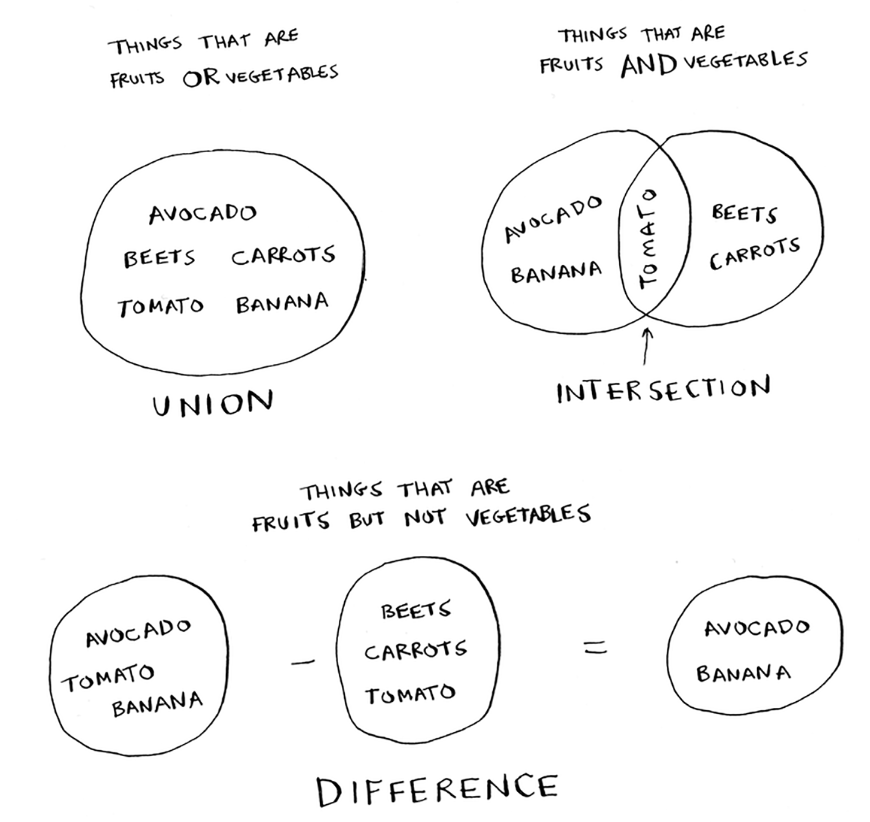
• Suppose you’re a greedy thief. You’re in a store with a knapsack. You can only take what you can fit in your knapsack (e.g. 35 lbs). You’re trying to maximize the value of the items you put in your knapsack.

• Greedy strategy:
  • Pick the most expensive thing that will fit in your knapsack.
  • Pick the next most expensive thing that will fit in your knapsack. And so on.

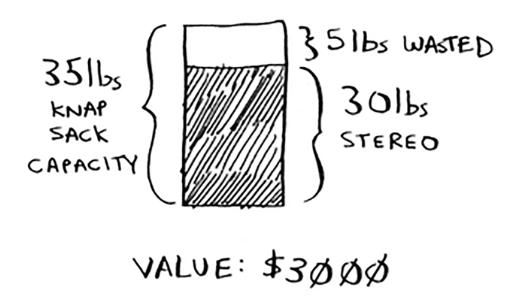
• Greedy strategy doesn’t give you the optimal solution. The most expensive item may weigh a lot, not leaving room for other items (stereo weights 30 lbs). However, “pretty good” is good enough.
  • Perfect is the enemy of good. Sometimes all you need is an algorithm that solves the problem pretty well. That is where greedy algorithms shine because they’re simple to write and usually get pretty close.

Set-covering problem

Suppose you’re starting a radio show. You want to reach listeners in all 50 states. Each station covers a region and there is overlap. What is the smallest set of stations you can play to cover all 50 states?

Brute force solution

1. List every possible subset of stations. This is called the power set. There are 2^n possible subsets.
2. From these, pick the set with the smallest number of stations that covers all 50 states.
   • The problem with brute force is that it takes a long time to calculate every possible set of stations. It takes O(2^n) time, because there are 2^n subsets.

   # of stations	# of subsets	O(2^n)
   5	32	2^5
   10	1024	2^10
   32	4 billion	2^32

Greedy algorithm solution

1. Pick the station that covers the most states that haven’t been covered yet. It’s ok if the station covers some states that have been covered already.
2. Repeat until all the states are covered.
   • This is called an approximation algorithm. When calculating the exact solution will take too much time, an approximation algorithm will work.
   • Approximation algorithms are judged by:
   • how fast they are
   • how close they are to the optimal solution - In this case, greedy algorithm runs in O(n^2) time where n is the number of stations.

Sets

• Union: combine both sets
• Intersection: find the items that show up in both sets
• Difference: subtract the items in one set from the items in the other set

NP-complete problems

• The traveling-salesperson problem and the set-covering problem both have something in common: you calculate every possible solution and pick the smallest/shortest one. Both of these problems are NP-complete.
• Traveling-salesperson problem
  • A salesperson has to visit five different cities. And he’s trying to figure out the shortest route that will take him to all five cities. To find the shortest route, you first have to calculate every possible route.
  • Factorial function is used to calculate the number of possible routes.

# of cities	# of routes
1	1	1!
2	2	2!
3	6	3!
4	24	4!
5	120	5!
6	720	6!
7	5040	7!
8	40320	8!

How do you tell if a problem is NP-complete?

There’s no easy way to tell if the problem you’re working on is NP-complete. Here are some giveaways:

• Your algorithm runs quickly with a handful of items but really slows down with more items.
• “All combinations of X” usually point to an NP-complete problem.
• If your problem involves a sequence (such as a sequence of cities, like traveling salesperson), and it’s hard to solve, it might be NP-complete.
• If your problem involves a set (like a set of radio stations) and it’s hard to solve, it might be NP-complete.
• Can you restate your problem as the set-covering problem or the traveling-salesperson problem? Then your problem is definitely NP-complete.