book-notes

Chapter 7 - Dijkstra’s algorithm

• Breadth-first search will find you the shortest path (path with the fewest segments).

  

• Dijkstra’s algorithm will find you the fastest path (path with the smallest total weight).

  

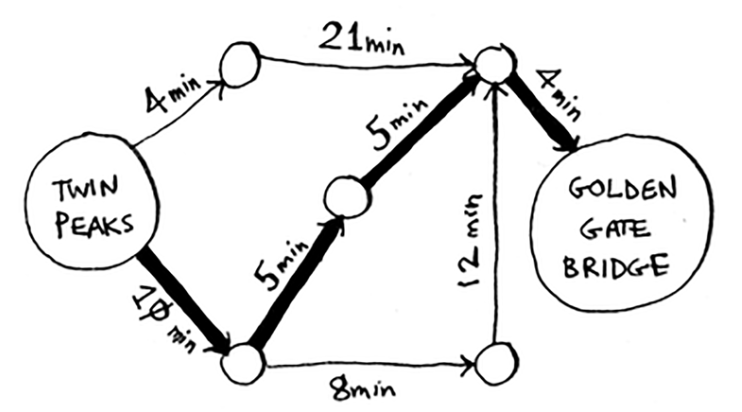
Working with Dijkstra’s algorithm

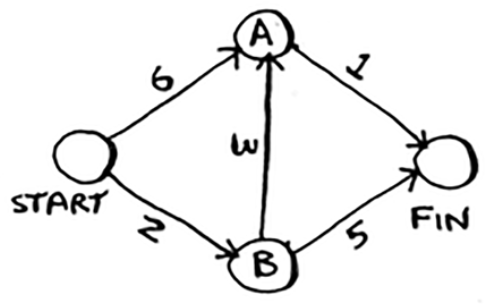
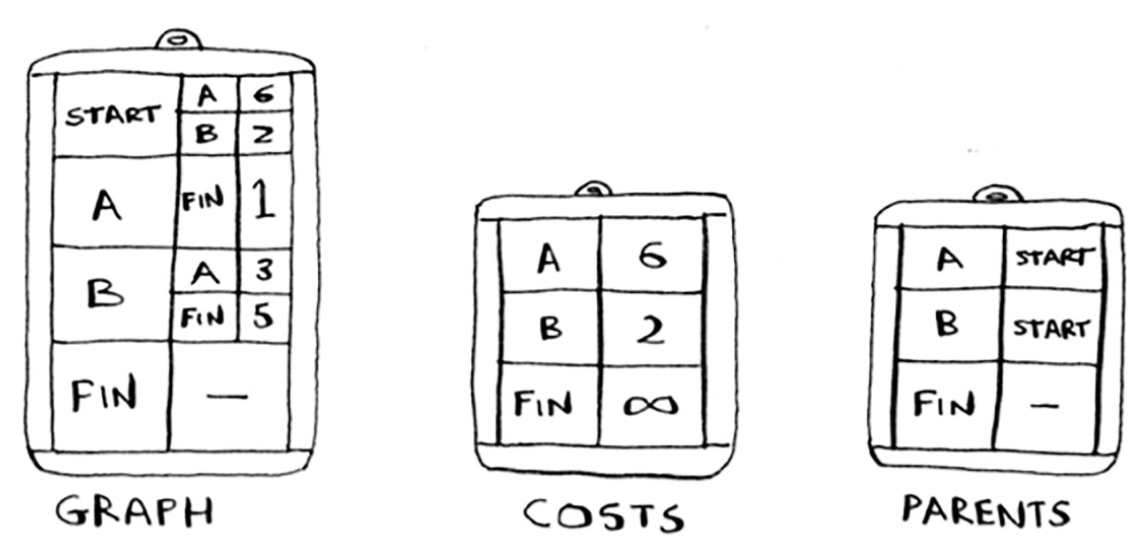
• You need 3 hash tables: graph, costs, parents
  • You will update the costs and parents as the algorithm progresses.
  • The cost of a node is how long it takes to get to that node from the start.
• You also need an array to keep track of all the nodes you’ve already processed, because you don’t need to process a node more than once.

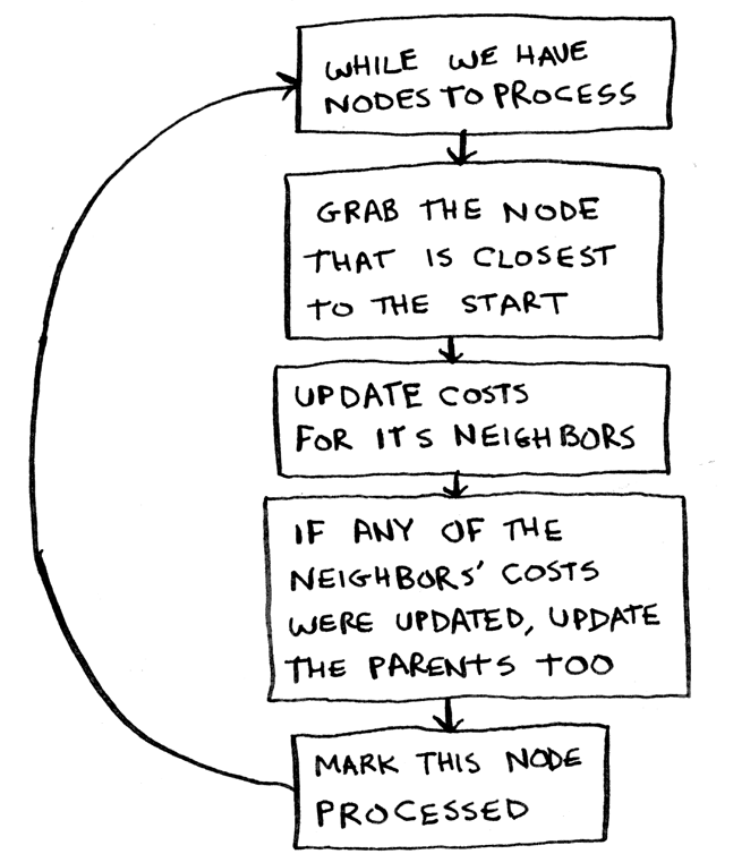
1. Find the cheapest node. This is the node you can get to in the least amount of time.
2. Check whether there’s a cheaper path to the neighbors of this node. If so, update their costs.
3. Repeat until you’ve done this for every node in the graph.
4. Calculate the final path.
   • Python implementation

    # Find the lowest cost node that you haven't processed yet
    node = find_lowest_cost_node(costs)
       
    # If you've processed all the nodes, the while loop is done
    while node is not None:
       
    	# Get the cost and neighbors of current node
    	cost = costs[node]
    	neighbors = graph[node]
       
    	# Loop through the neighbors
    	for n in neighbors.keys():
    		new_cost = cost + neighbors[n]
       
    		# If it's cheaper to get to the neighbor by going through current node,
    		# update the cost for the neighbor
    		if costs[n] > new_cost:
    			costs[n] = new_cost
    			parents[n] = node
       
    	# Mark the node as processed
    	processed.append(node)
       
    	# Find the next node to process
    	node = find_lowest_cost_node(costs)
   

• Javascript implementation

    const graph = {
      start: {
        a: 6,
        b: 2
      },
      a: {
        finish: 1
      },
      b: {
        a: 3,
        finish: 5
      },
      finish: {}
    };
      
    const costs = {
      a: 6,
      b: 2,
      finish: Infinity
    };
      
    const parents = {
      a: "start",
      b: "start",
      finish: null
    };
      
    function findShortestPath(graph) {
      let processed = [];
      
      // Find the lowest cost node that you haven't processed yet
      let node = findLowestCostNode(costs, processed);
      
      // If you've processed all the nodes, the while loop is done
      while (node) {
        // Get the cost and neighbors of current node
        const cost = costs[node];
        const neighbors = graph[node];
      
        // Loop through the neighbors
        for (const neighbor in neighbors) {
          const oldCost = costs[neighbor];
          const newCost = cost + neighbors[neighbor];
      
          // If it's cheaper to get to the neighbor by going through current node,
    			// update the cost for the neighbor
          if (newCost < oldCost) {
            costs[neighbor] = newCost;
            parents[neighbor] = node;
          }
        }
      
        // Mark the node as processed
        processed.push(node);
      
        // Find the next node to process
        node = findLowestCostNode(costs, processed);
      }
      
      return costs.finish;
    }
      
    function findLowestCostNode(costs, processed) {
      let lowestCost = Infinity;
      let lowestCostNode = null;
      
      for (const node in costs) {
        const cost = costs[node];
      
        if (!processed.includes(node) && cost < lowestCost) {
          lowestCost = cost;
          lowestCostNode = node;
        }
      }
      
      return lowestCostNode;
    }
  

Terminology

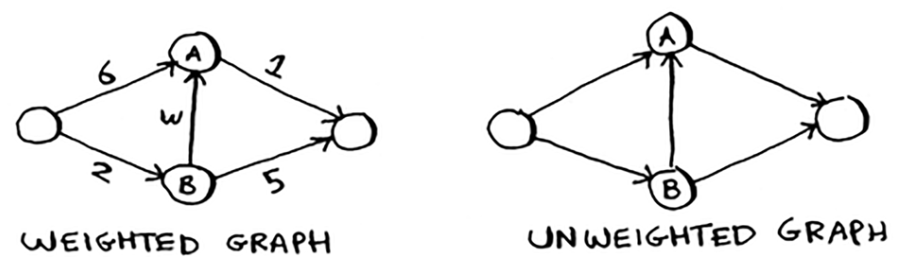
• Weight is assigned to each edge of the graph.
• Weighted graph is a graph with weights. Use Dijkstra to calculate the shortest path.
• Unweighted graph is a graph without weights. Use BFS to calculate the shortest path.

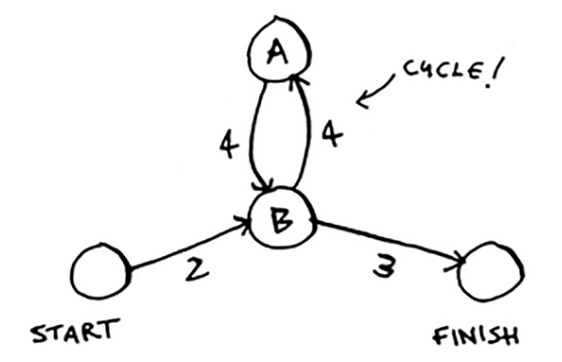
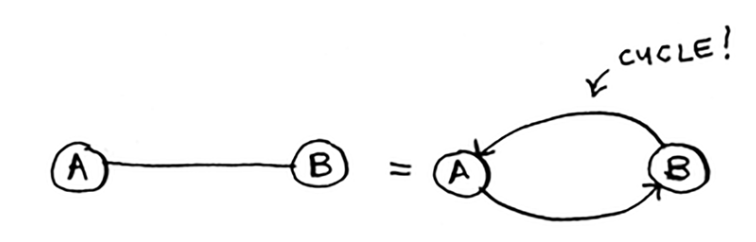
• Cycle in a graph happens when you start at a node, travel around, and end up at the same node.

  

  • Undirected graph is an example of a cycle.

  

• Dijkstra only works on graphs with no cycles, or on graphs with a positive weight cycle.

Negative-weight edges

• You can’t use Dijkstra if you have negative-weight edges. Negative-weight edges break the algorithm.

  • Negative-weight edges break the algorithm when the same node has to be processed twice.

    

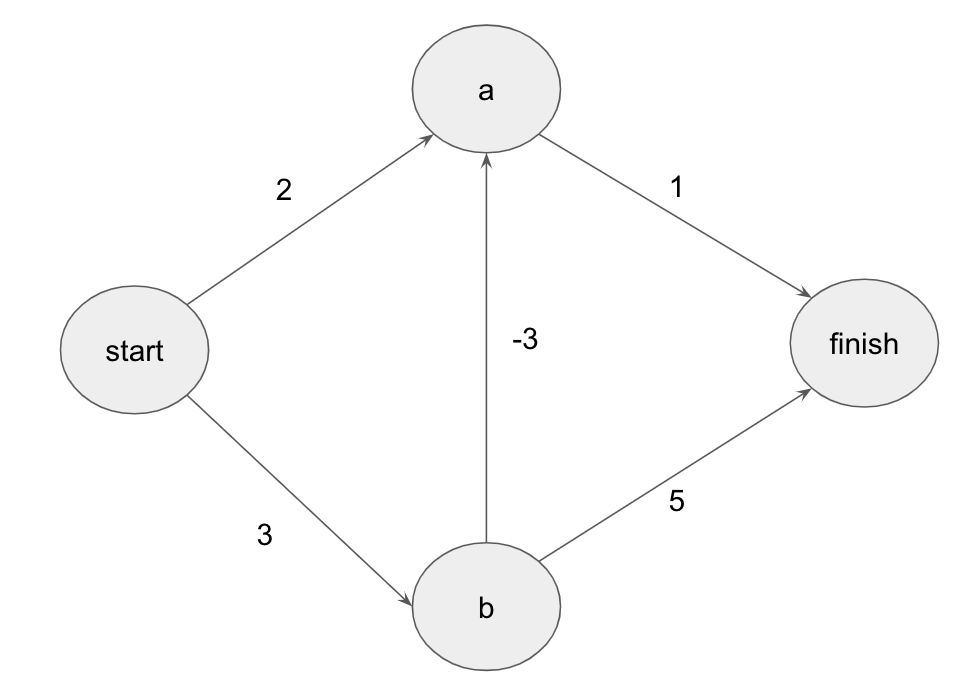
• Use Bellman-ford algorithm if you want to find the shortest path in a graph that has negative-weight edges.

Recap

• BFS is used to calculate the shortest path for an unweighted graph.
• Dijkstra is used to calculate the shortest path for a weighted graph.
• Dijkstra works when all the weights are positive.
• Use the Bellman-ford algorithm if you have negative weights.

Notes: https://medium.com/basecs/finding-the-shortest-path-with-a-little-help-from-dijkstra-613149fbdc8e